Детям в школе приходится несладко: то сменку забыл, то домашки много задали. А когда дело доходит до изучения математики, так большинство вообще не знают, за что хвататься первым делом и как разобраться со сложными цифрами, формулами и другими закорючками.
Но есть несколько приемов, которые смогут хоть немного упростить жизнь любого школьника, особенно, если на уроках запрещают пользоваться калькуляторами. Именно о них мы тебе сейчас и расскажем.

- 1. Возведение в квадрат чисел, которые оканчиваются на 5
- 2. Возведение в квадрат двузначных чисел
- 3. Умножение двузначных чисел на 11
- 4. Сложное умножение
- 5. Умножение чисел, состоящих из единиц, на самих себя
- 6. Умножение трехзначных чисел на однозначные
- 7. Как найти процент от большого числа
- 8. Табличка умножения на 9
- 9. Деление чисел на 5
- 10. Магическое число 1 089
1. Возведение в квадрат чисел, которые оканчиваются на 5
Любое двузначное число, оканчивающееся на 5, легко возвести в квадрат, нужно лишь первую цифру числа (десятки) умножить на цифру большую на единицу, а потом к полученному значению приписать в конце 25. Например, в квадрат нужно возвести 65: Первый шаг: 6 х 7 = 42. Второй шаг: дописываем 25, получаем 4 225.

2. Возведение в квадрат двузначных чисел
Квадрат сложного двузначного числа можно найти без особого труда, если оно находится рядом с тем, квадрат которого посчитать совсем просто.
Нужно к квадрату числа, на единицу меньше исходного, прибавить это же уменьшенное на единицу число и само исходное. Например, в квадрат нужно возвести 41: 41^2 = 40^2 + 40 + 41 = 1 600 + 81 = 1 681.
3. Умножение двузначных чисел на 11
Чтобы быстро умножить двузначное число на 11, нужно просто сложить его цифры. Если сумма получается однозначной, то мы просто вписываем ее между цифрами исходного числа. Например, 63 х 11 = 693 (9 = 3 + 6).
Если сумма получается двузначной, то алгоритм усложняется на 1 шаг. Последнюю цифру суммы мы так и вписываем между цифрами исходного числа, а первая цифра суммы — всегда единица, поскольку сумма любых двух цифр не может превышать 18 (9 + 9).
И эту единицу мы просто прибавляем к первой цифре исходного числа. Например: 93 х 11 = 9(12)3 = 1 023.
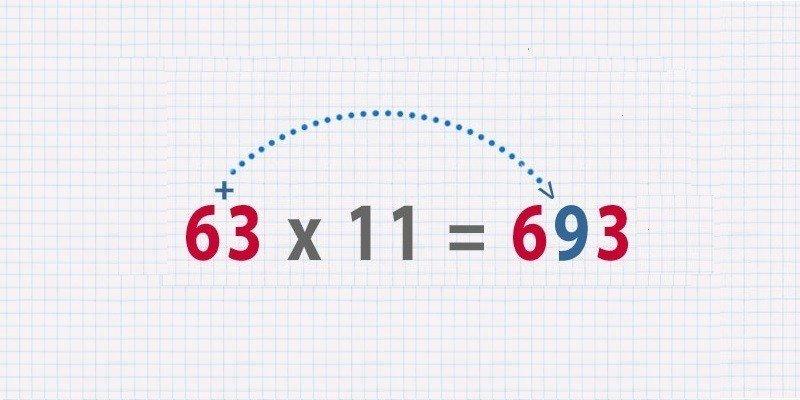
4. Сложное умножение
В некоторых ситуациях перемножить числа между собой помогает разложение их на простые множители. Например, 16 х 225 = (2 х 2 х 2 х 2) х 225.
Дальше каждую двойку по отдельности умножаем на число, и найти результат оказывается не так уж сложно. 2 х 2 х 2) х (2 х 225) = (2 х 2) х (2 х 450) = 2 х (2 х 900) = 2 х 1 800 = 3 600.
5. Умножение чисел, состоящих из единиц, на самих себя
Чем объяснять закономерность словами, проще проследить ее наглядно на этой таблице. Главное — правильно посчитать количество единиц в числе.

6. Умножение трехзначных чисел на однозначные
Всё гениальное просто, тебе нужно лишь разбить «страшное» трехзначное число на составляющие попроще. Например, 284 х 3 = (200 + 80 + 4) х 3 = (200 х 3) + (80 х 3) + (4 х 3) = 600 + 240 + 12 = 852.

7. Как найти процент от большого числа
Чтобы упростить себе задачу, и число, и сам процент раздели на 10, а потом перемножь результаты между собой. Например, 70 % от 300: 7 х 30 = 210.
8. Табличка умножения на 9
Если трудно зазубрить значения, нам на помощь приходят руки. Смотрим на ладони и загибаем палец, который по счету соответствует цифре-множителю.
Количество пальцев перед ним — это десятки, а после него — единицы в результате умножения. Например, 6 х 9 = 54 (5 пальцев до и 4 после загнутого пальца).

9. Деление чисел на 5
Чтобы быстро и легко поделить большое число на 5, нужно просто умножить его на 2 и запятой «отодвинуть» последний знак. Например, нам нужно 341 разделить на 5. Умножаем 341 на 2 и получаем 682. Переносим запятую на один знак вперед и получаем 68,2.

10. Магическое число 1 089
Ну и напоследок, не столько лайфхак, сколько интересная закономерность, которой можно лишний раз заинтересовать ребенка математикой.
Нужно взять любое трехзначное число, цифры которого идут в порядке убывания (например, 431 или 863), и отнять от него число, записанное теми же цифрами, но в обратном порядке.
Потом к полученной разнице нужно прибавить число, записанное в обратном порядке, но уже ее цифрами разницы. И полученная сумма всегда будет равна 1 089.
Проверим цифры с нашего примера: 431 – 134 = 297. Прибавляем к результату его «зеркальное» значение: 297 + 792 = 1 089. Второй пример: 863 – 368 = 495. 495 + 594 = 1 089. И так можно продолжать бесконечно, результат всегда будет 1 089.

Вот так, благодаря нескольким хитростям математика вмиг может стать любимой наукой не только для ребенка, но и для взрослого.
Учеба в школе была бы куда проще и увлекательнее, если бы такие закономерности показывали и объясняли на уроках. Не зря математику называют царицей наук, в ней сокрыто множество удивительных, но при этом абсолютно логичных вещей.








